Карактеристике хептагоналне призме и како израчунати обим
А хептагонал присм је геометријска фигура која, као што име имплицира, укључује две геометријске дефиниције које су: призма и хептагон.
"Призма" је геометријска фигура ограничена двјема базама које су једнаки и паралелни полигони и њихове бочне стране су паралелограми.
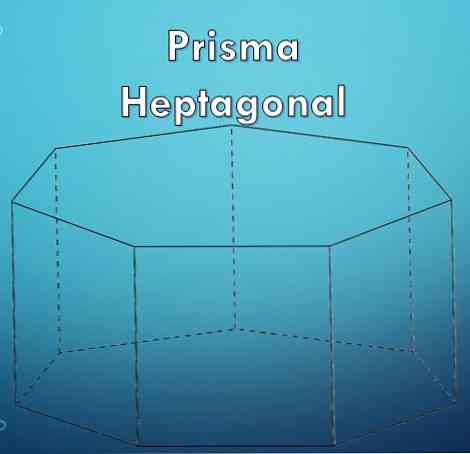
"Хептагон" је полигон који је формиран са седам (7) страна. Пошто је хептагон полигон, може бити да је редован или неправилан.
За полигон се каже да је правилан ако све његове стране имају исту дужину и њихови унутрашњи углови мјере исто, називају се и једнакостранични полигони; у супротном се каже да је полигон неправилан.

Карактеристике хептагоналне призме
Слиједе одређене карактеристике које имају хептагоналну призму као што су: њена конструкција, својства база, површина свих његових лица и њен волумен.
1- Цонструцтион
За изградњу седмерокутне призме потребна су два хептагона, која ће бити њене базе и седам паралелограма, по један на свакој страни шестерокута.
Почните са цртањем хептагона, затим нацртајте седам вертикалних линија, једнаке дужине, које долазе из сваког од његових врхова.
Коначно, други хептагон је нацртан тако да се његови врхови поклапају са крајем црта нацртаних у претходном кораку.
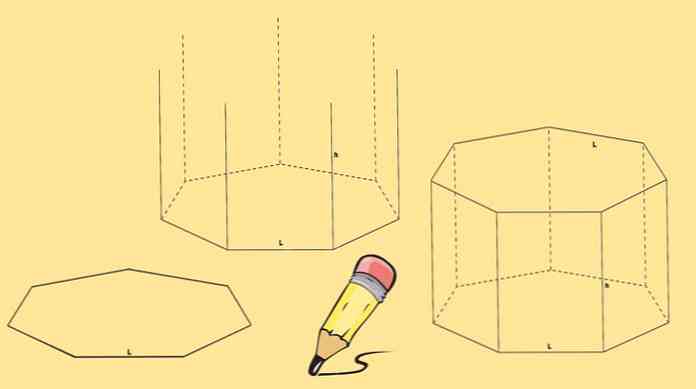
Хептагоналну призму која је повучена изнад назива се равна хептагонална призма. Али можете имати и косу хептагоналну призму као на следећој слици.

2. Својства база
Пошто су њихове базе хептагони, они одговарају да је дијагонални број Д = нк (н-3) / 2, где је "н" број страна полигона; у овом случају имамо Д = 7 × 4/2 = 14.
Такође можемо видети да је сума унутрашњих углова било којег хептагона (регуларног или неправилног) једнака 900º. Ово се може потврдити следећом сликом.
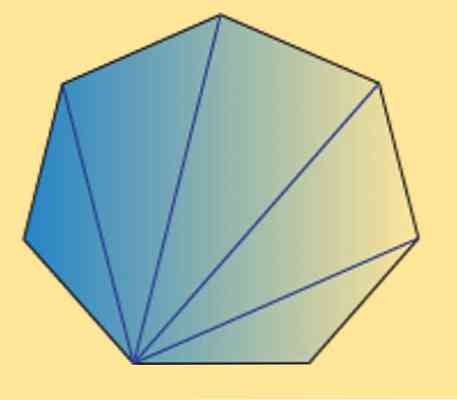
Као што видите, постоји 5 унутрашњих троуглова, а коришћењем сума унутрашњих углова троугла једнако је 180º, може се добити да је жељени резултат.
3. Подручје које је потребно за изградњу хептагоналне призме
Пошто су његове основе две хептагоне и његове стране су седам паралелограма, површина потребна за конструкцију хептагоналне призме је једнака 2кХ + 7кП, где је "Х" површина сваког хептагона и "П" површина сваког паралелограма.
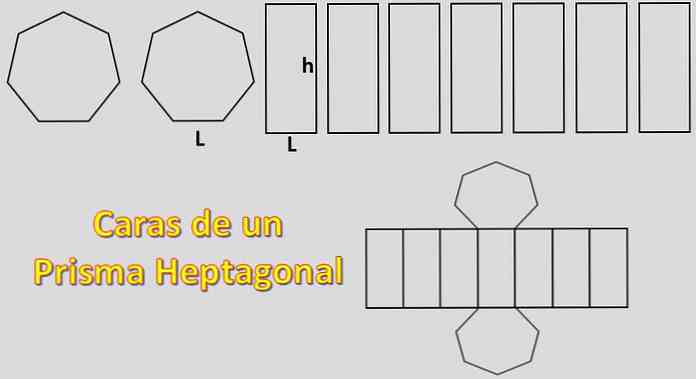
У овом случају, израчунава се површина регуларног хептагона. За ово је важно знати дефиницију апотме.
Апотхем је окомита линија која иде од центра регуларног полигона до средине било које његове стране.
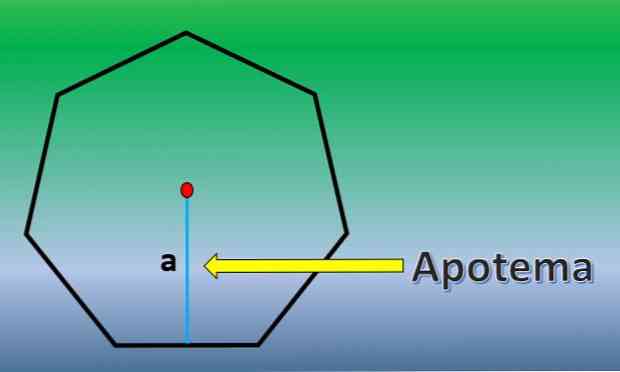
Када је апотем познат, површина хептагона је Х = 7кЛка / 2, где је "Л" дужина сваке стране и "а" дужина апотема..
Подручје паралелограма је лако израчунати, дефинисано је као П = Лкх, где је "Л" иста дужина бочне стране шестерокута и "х" је висина призме.
У закључку, количина материјала потребног за изградњу хептагоналне призме (са регуларним базама) је 7кЛка + 7кЛкх, то јест, 7кЛ (а + х).
4- Волуме
Једном када је површина базе и висина призме позната, волумен је дефинисан као (основна површина) к (висина).
У случају хептагоналне призме (са регуларном базом) она има свој волумен В = 7кЛкакх / 2; такође се може написати као В = Пкакх / 2, где је "П" периметар регуларног хептагона.
Референце
- Биллстеин, Р., Либескинд, С., & Лотт, Ј.В. (2013). Математика: приступ рјешавања проблема за наставнике основног образовања. Лопез Матеос Едиторес.
- Фрегосо, Р.С., & Царрера, С.А. (2005). Математика 3. Едиториал Прогресо.
- Галлардо, Г., & Пилар, П. М. (2005). Математика 6. Едиториал Прогресо.
- Гутиеррез, Ц.Т., & Циснерос, М. П. (2005). Трећи курс математике. Едиториал Прогресо.
- Кинсеи, Л., & Мооре, Т.Е. (2006). Симетрија, облик и простор: Увод у математику кроз геометрију (илустровано, репринт ед.). Спрингер Сциенце & Бусинесс Медиа.
- Митцхелл, Ц. (1999). Даззлинг Матх Лине Десигнс (Иллустратед ед.). Сцхоластиц Инц.
- Р., М. П. (2005). Ја цртам 6º. Едиториал Прогресо.


