Броглие Атомиц Модел Цхарацтеристицс анд Лимитатионс

Тхе Броглиеов атомски модел је предложио француски физичар Лоуис Броглие 1924. године. У својој докторској тези Броглие је потврдио дуалност таласа и честица електрона, постављајући темеље таласне механике. Броглие је објавио важне теоријске спознаје о природи материје у таласној маси на атомској скали.

Након тога, научници Клинтон Дависон и Лестер Гермер су 1927. године експериментално демонстрирали Броглиеве изјаве..

Броглие је најавио могућност да материја има понашање слично ономе светлости, и сугерисао сличне особине у субатомским честицама као што су електрони.

Електрични набоји и орбите ограничавају амплитуду, дужину и фреквенцију таласа који описују електрони. Броглие је објаснио кретање електрона око атомског језгра.

Индек

• 1 Карактеристике Броглиејевог атомског модела
• 2 Дависонов и Гермер експеримент
• 3 Ограничења
• 4 Чланци од интереса
• 5 Референце

Карактеристике Броглиејевог атомског модела

Да би развио свој предлог, Броли је кренуо од принципа да електрони имају двоструку природу између таласа и честице, слично светлу.

У том смислу, Броглие је направио поређење између оба феномена и на основу једначина које је развио Ајнштајн за проучавање таласне природе светлости, он је указао на следеће:

- Укупна енергија фотона и, сходно томе, укупна енергија електрона, резултат је производа фреквенције вала и константе Планка (6.62606957 (29) × 10). ^-34 Јулес к секунди), као што је детаљно описано у следећем изразу:

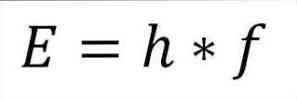
У овом изразу:

Е = енергија електрона.

х = Константа даске.

ф = фреквенција таласа.

- Линеарни моменат фотона, па самим тим и електрона, обрнуто је пропорционалан таласној дужини, а обје магнитуде се односе на константу Планк:

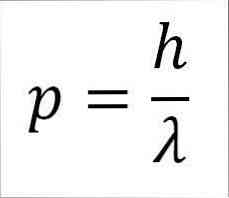
У овом изразу:

п = линеарни моменат електрона.

х = Константа даске.

λ = таласна дужина.

- Линеарни моменат је продукт масе честице брзином коју та честица има током свог помака.

Ако се претходни математички израз реструктурира као функција таласне дужине, имамо следеће:

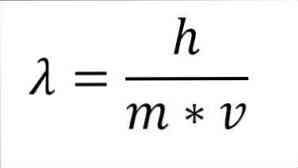
У наведеном изразу:

λ = таласна дужина.

х = Константа даске.

м = маса електрона.

в = брзина електрона.

Пошто х, константа Планка, има малу вредност, таласна дужина λ је такође. Сходно томе, могуће је рећи да се таласна својства електрона јављају само на атомском и субатомском нивоу.

- Броглие се такође заснива на постулатима Боровог атомског модела. Према потоњем, орбите електрона су ограничене и могу бити само многоструке целих бројева. Тако:

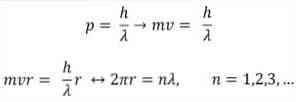
Где:

λ = таласна дужина.

х = Константа даске.

м = маса електрона.

в = брзина електрона.

р = радијус орбите.

н = цео број.

Према Боровом атомском моделу, који је Броглие усвојио као основу, ако се електрони понашају као стојећи валови, једине дозвољене орбите су оне чији је радијус једнак интегралном вишку таласне дужине λ..

Према томе, нису све орбите испуниле параметре неопходне за кретање електрона кроз њих. Зато електрони могу путовати само у одређеним орбитама.

Таласна теорија Броглиејевих електрона оправдала је успех Бохровог атомског модела да би објаснила понашање једног електрона водониковог атома..

Аналогно томе, такође је расветљено зашто овај модел није одговарао сложенијим системима, тј. Атомима са више од једног електрона.

Дависсон и Гермер експеримент

Експериментална верификација Броглиејевог атомског модела догодила се 3 године након објављивања, 1927.

Угледни амерички физичари Цлинтон Ј. Дависсон и Лестер Гермер експериментално су потврдили теорију валне механике.

Дависсон и Гермер извели су тестове расипања електронског снопа кроз кристал никла и уочили феномен дифракције кроз метални медиј.

Проведени експеримент се састојао од провођења сљедеће процедуре:

- У првом случају, постављен је склоп са електронским снопом који је имао познату почетну енергију.

- Инсталиран је извор напона за убрзавање кретања електрона, што је довело до потенцијалне разлике.

- Ток електронског снопа био је усмерен ка металном кристалу; у овом случају, никл.

- Мјерен је број електрона који су утјецали на кристал никла.

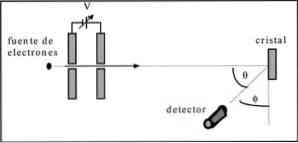
На крају експеримента, Дависсон и Гермер су открили да су електрони распршени у различитим правцима.

Понављајући експеримент користећи металне кристале различитих оријентација, научници су открили следеће:

- Дисперзија електронског снопа кроз метални кристал је била упоредива са појавом интерференције и дифракције светлосних зрака.

- Одраз електрона на кристалу удара описао је путању која, теоретски, треба описати према теорији електронских таласа Броглие-а..

У синтези, експеримент Дависона и Гермера експериментално је доказао дуалну таласну честицу електрона.

Ограничења

Броглијев атомски модел не предвиђа тачну локацију електрона на орбити у којој се креће.

У овом моделу, електрони се перципирају као таласи који се крећу око орбите без специфичне локације, што уводи концепт електронске орбите.

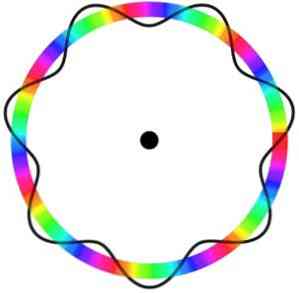
Поред тога, Броглиејев атомски модел, аналоган Сцхродингеровом моделу, не разматра ротацију електрона на својој оси (спин).

Игнорирајући унутрашњи угаони момент електрона, просторне варијације ових субатомских честица се занемарују..

У истом редоследу идеја, овај модел не узима у обзир промене у понашању брзих електрона као последица релативистичких ефеката..

Чланци од интереса

Атомски модел Шредингера.

Атомски модел Цхадвицка.

Атомски модел Хеисенберга.

Атомски модел Перрина.

Атомски модел Тхомсона.

Атомски модел Далтона.

Атомски модел Дирац Јордан.

Атомски модел Демокрита.

Атомски модел Бохра.

Референце

1. Борове квантне теорије и Де Броглие Вавес (с.ф.). Преузето са: не.пхис.киусху-у.ац.ј
2. Лоуис де Броглие - Биограпхицал (1929). © Тхе Нобел Фоундатион. Преузето са: нобелпризе.орг
3. Лоуис-Вицтор де Броглие (с.ф.). Преузето са: цхемед.цхем.пурдуе.еду
4. Ловетт, Б. (1998). Лоуис де Броглие. Енцицлопӕдиа Британница, Инц Добављено из: британница.цом
5. Атомски модел Де Броглие. Национални универзитет за образовање на даљину. Шпанија Преузето са: оцв.иннова.унед.ес
6. Вавес оф Маттер Оф Лоуис Де Броглие (с.ф.). Добављено из: хиру.еус
7. Вон Памел, О., и Марцхисио, С. (с.ф.). Квантна механика Национални универзитет Росарио. Добављено из: фцеиа.унр.еду.ар