Карактеристике капиларности и пример у води
Тхе капиларност То је својство течности која им омогућава да се крећу кроз цевасте рупе или порозне површине чак и против силе гравитације. За то, мора постојати равнотежа и координација две силе везане за течне молекуле: кохезија и адхезија; имају ова два физичка рефлексија названа површинска напетост.
Течност мора бити способна да мокри унутрашње зидове цеви или поре материјала кроз који се креће. Ово се дешава када је сила адхезије (течни зид капиларне цеви) већа од интермолекуларне кохезионе силе. Сходно томе, течни молекули стварају јачу интеракцију са атомима материјала (стакло, папир, итд.) Него између њих.
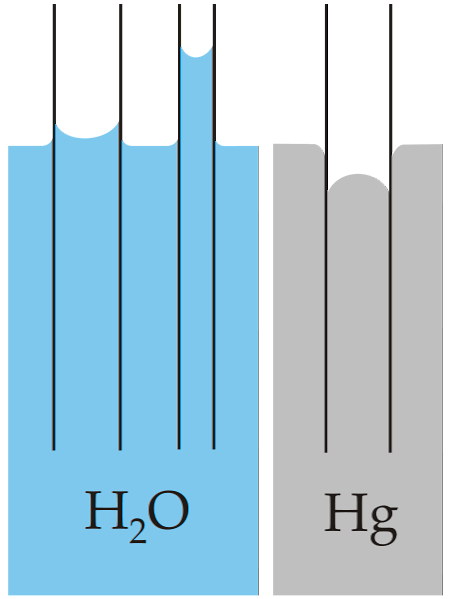
Класични пример капиларности је илустрован у поређењу ове особине за две веома различите течности: воду и живу.
Горња слика показује да се вода диже кроз зидове цијеви, што значи да има веће силе приањања; док се супротно дешава са живом, јер њене кохезивне, металне силе спајања спречавају влажење стакла.
Због тога вода формира конкавни мениск, а жива конвексни мениск (куполасти облик). Такође треба напоменути да што је мањи полупречник цеви или одељка кроз који се течност креће, већа је висина или пређена удаљеност (упоредите висину водених стубова за обе цеви)..
Индек
- 1 Карактеристике капиларности
- 1.1 - Површина течности
- 1.2 -Хигхт
- 1.3 - Површинска напетост
- 1.4 -Радио капиларе или пора где се течност диже
- 1.5 - Угао контакта (θ)
- 2 Капиларност воде
- 2.1 О биљкама
- 3 Референце
Карактеристике капиларности
-Површина течности
Површина течности, рецимо вода, у капилари је конкавна; менискус је конкаван. Оваква ситуација се дешава зато што је резултирајуће силе на молекуле воде близу зида цеви усмерене ка томе.
У свим менискусима постоји контактни угао (θ), који представља угао који формира зид капиларне цеви са линијом која се додирује са површином течности у тачки контакта.
Снаге адхезије и кохезије
Ако сила адхезије течности на капиларни зид превладава над интермолекуларном кохезионом силом, онда је угао θ < 90º; el líquido moja la pared capilar y el agua asciende por el capilar, observándose el fenómeno conocido como capilaridad.
Када се кап воде стави на површину чистог стакла, вода се шири на стакло, тако да θ = 0 и цос θ = 1.
Ако сила интерголекуларне кохезије превладава над адхезионом снагом капиларе у течном зиду, на пример у живу, мениск је конвексан и угао θ ће имати вредност> 90º; жива не мокри капиларни зид и стога се спушта кроз његов унутрашњи зид.
Када се капљица живе стави на површину чистог стакла, капљица задржава свој облик и угао θ = 140º.
-Висина
Вода се диже кроз капиларну цев да достигне висину (х), у којој тежина воденог стуба компензује вертикалну компоненту силе међумолекуларне кохезије.
Како се више воде диже, доћи ће до тачке у којој ће гравитација зауставити њен раст, чак и када површинска напетост ради у вашу корист.
Када се то догоди, молекули не могу наставити да се пењу по унутрашњим зидовима, и све физичке силе су изједначене. С једне стране имате силе које промовишу уздизање воде, ас друге стране, ваша властита тежина га гура.
Јуринов закон
Ово се може написати математички на следећи начин:
2 π рΥцосθ = ρгπр2х
Тамо где лева страна једначине зависи од површинске напетости, чија је величина такође повезана са кохезионом или интермолекуларном силом; Цосθ представља контактни угао, а р полупречник рупе кроз коју се течност диже.
А на десној страни једначине имамо висину х, силу гравитације г и густину течности; то би била вода.
Очистите онда х имате
х = (2Υцосθ / ρгр)
Ова формулација је позната као Јуринов закон, који дефинира висину која се постиже колоном течности, у капиларној цијеви, када је тежина колоне течности уравнотежена са силом ускрснућа капиларно.
-Сурфаце тенсион
Вода је диполарни молекул, због електронегативности атома кисеоника и његове молекуларне геометрије. Ово доводи до тога да је део молекула воде где се налази кисеоник негативно наелектрисан, док је део молекула воде, који садржи 2 атома водоника, позитивно наелектрисан..
Молекули унутар течности међусобно дјелују захваљујући вишеструким водиковим везама, држећи их заједно. Међутим, молекули воде који се налазе у површини воде: ваздух (површина), подложни су нето привлачењу молекула течног синуса, који нису компензовани слабом атракцијом молекула ваздуха..
Због тога, молекули воде на интерфејсу су подвргнути привлачној сили која тежи да уклони молекуле воде из интерфејса; то јест, водонични мостови формирани са молекулима у дну повлаче оне који су на површини. Према томе, површинска напетост настоји смањити површину сучеља воде: зрак.
Однос са х
Ако погледате једначину Јуриновог закона, наћи ћете да је х директно пропорционалан Υ; према томе, што је већа површинска напетост течности, већа је висина која може да се издигне кроз капилару или поре материјала.
Према томе, може се очекивати да се за две течности, А и Б, са различитим површинским напетостима, она са највећом површинском напетошћу подиже на вишу висину..
Из ове тачке се може закључити да је висока површинска напетост најважнија карактеристика која одређује капиларно својство течности.
-Радијус капиларе или пора где се течност диже
Посматрање Закона Јурина указује на то да је висина коју је достигла течност у капилари или пори обрнуто пропорционална радијусу исте.
Дакле, што је мањи радијус, то је већа висина коју ће колона течности постићи капиларним дејством. Ово се може видети директно на слици где се вода упоређује са живом.
У стакленој цијеви у радијусу радијуса 0,05 мм, водени ступац капиларношћу ће достићи висину од 30 цм. У капиларним цевима радијуса од 1 μм са усисним притиском од 1,5 к 103 хПа (која је једнака 1,5 атм) одговара израчуну висине воденог стуба од 14 до 15 м.
Ово је веома слично ономе што се дешава са оним сламкама које се неколико пута окрећу. Усисавањем течности настаје разлика у притиску због које се течност подиже у уста.
Максимална вриједност висине ступца постигнута капиларношћу је теоријска, јер се радијус капилара не може смањити изнад одређене границе.
Лав оф Поисеуилле
Овим се утврђује да је проток реалне течности дат следећим изразом:
К = (πр4/ 8ηл) ΔП
Гдје је К проток текућине, η је његов вискозитет, л дужина цијеви, а ΔП разлика тлака.
Када се смањује радијус капиларе, висина колоне течности коју достигне капиларност треба да се повећава неограничено. Међутим, Поисеуилле истиче да смањење радијуса такође смањује проток течности кроз ту капилару.
Поред тога, вискозност, која је мера отпорности која се супротставља протоку стварне течности, додатно би смањила проток течности.
-Угао контакта (θ)
Што је виша вредност цосθ, већа је висина воденог стуба по капиларности, као што је назначено Јуриновим законом.
Ако је θ мали и приближава се нули (0), цосθ је = 1, тако да је вредност х максимална. Напротив, ако је θ једнако 90º, цосθ = 0 и вредност х = 0.
Када је вредност θ већа од 90º, што је случај са конвексним менискусом, течност се не повећава капиларно и њена тенденција је да се спусти (као што се дешава са живом).
Капиларност воде
Вода има површинску напетост од 72,75 Н / м, релативно високу у односу на вредности за површинску напетост следећих течности:
-Ацетон: 22,75 Н / м
-Етилни алкохол: 22,75 Н / м
-Хексан: 18.43 Н / м
-Метанол: 22,61 Н / м.
Због тога вода има изузетну површинску напетост, што погодује развоју капиларног феномена тако неопходног за апсорпцију воде и хранљивих материја у биљкама..
На биљке

Капиларност је важан механизам за подизање сока од стране ксилема биљака, али је сам по себи недовољан да би сап дохватио лишће дрвећа..
Транспирација или испаравање је важан механизам у успону сакса помоћу ксилема биљака. Лишће губи воду испаравањем, стварајући смањење количине молекула воде, што узрокује привлачење молекула воде присутних у капиларним цјевчицама (ксилем).
Молекули воде не делују независно један од другог, већ делују по Ван дер Ваалсовим силама, што доводи до тога да се уздижу повезане капиларним цевима биљака према листовима..
Поред ових механизама, треба напоменути да биљке апсорбују воду из тла путем осмозе и да позитивни притисак генерисан у корену, покреће почетак успона воде кроз капиларе биљке..
Референце
- Гарциа Францо А. (2010). Површне појаве. Добављено из: сц.еху.ес
- Феномен површине: површинска напетост и капиларност. [ПДФ] Добављено из: угр.ес
- Википедиа. (2018). Капиларност Преузето са: ен.википедиа.орг
- Рисвхан Т. (с.ф.) Капиларност у биљкама. Преузето са: ацадемиа.еду
- Хелменстине, Анне Марие, Пх.Д. (22. децембар 2018). Капиларна акција: дефиниција и примјери. Преузето са: тхоугхтцо.цом
- Еллен Еллис М. (2018). Капиларна активност воде: Дефиниција и примјери. Студија. Преузето са: студи.цом
- СциенцеСтруцк Стафф. (16. јул 2017.) Примери који објашњавају концепт и значење капиларне акције. Преузето са: сциенцеструцк.цом


