Колико рубова има хексагонална призма?
То кнов колико рубова има хексагонална призма значење "ивице", "призме" и "шестерокута" мора бити познато. Прва два концепта су опште дефиниције, а трећи појам има облик геометријске фигуре.
Када говоримо о шестерокуту, спомиње се шестерокут (полигон). Префикс "хека" означава да полигон има шест страна.

Руб је ивица објекта. Геометријски, то је линија која спаја две узастопне тачке геометријске фигуре.
Призма је геометријска фигура ограничена двјема базама које су паралелне и једнаке полигоне, а њихове бочне стране су паралелограми.
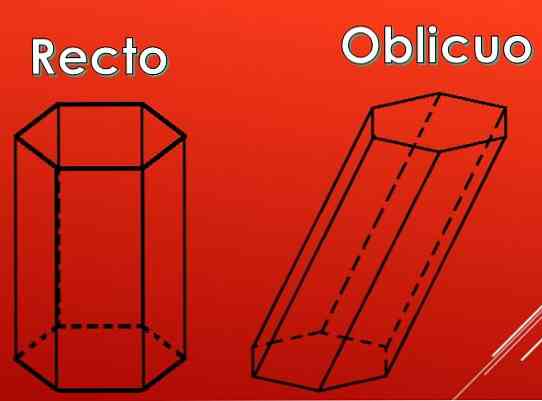
На следећој слици може се видети да бочне стране шестерокутне призме могу бити правоугаоници, али могу бити и паралелограми..
Према типу паралелограма, премије се могу сврстати у два типа: равна и коса.
Како бројати ивице шестерокутне призме?
Број ивица које ће имати хексагонална призма неће се променити ако је у питању равна или коса призма. Такође, број ивица не зависи ни од дужине страница.
Бројање ивица шестерокутне призме може се извршити на неколико начина. Ево два начина:
1- Разлагање призме
Један од начина да се изброје ивице је разлагање шестерокутне призме у њене две базе и бочне стране. На тај начин добијате два шестерокута и паралелограм са пет унутрашњих линија.
Сваки шестерокут има шест ивица, тако да ће призма имати више од 12 ивица.
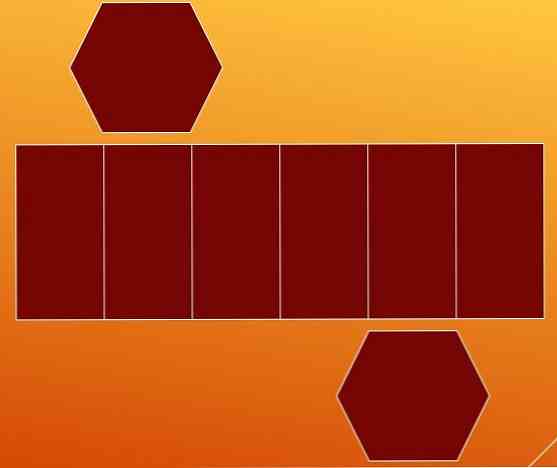
На први поглед се сматра да паралелограм садржи девет ивица (седам вертикалних и два хоризонтална). Али, погодно је да престанете да анализирате овај случај.
Када је паралелограм савијен тако да формира призму, може се видети да ће се прва линија на левој страни спојити са последњом линијом на десној страни, са којом обе линије представљају једну ивицу..
Али шта је са две хоризонталне линије?
Када се сви делови поново споје, хоризонталне линије ће бити спојене, свака са шест ивица сваког шестерокута. Из тог разлога, бројање би било погрешно.
Дакле, паралелограм садржи шест ивица призме које заједно са 12 ивица броје на почетку, даје укупно 18 ивица.
2.- Пројицирање сваке ивице
Други начин, много једноставнији за бројање ивица, користи чињеницу да су базе хексагоналних призми шестерокути, а свака база има шест ивица.
С друге стране, са сваког врха шестерокута, једна ивица је пројектована на одговарајући врх другог хексагона; то јест, постоји шест ивица које се спајају са једном базом са другом.
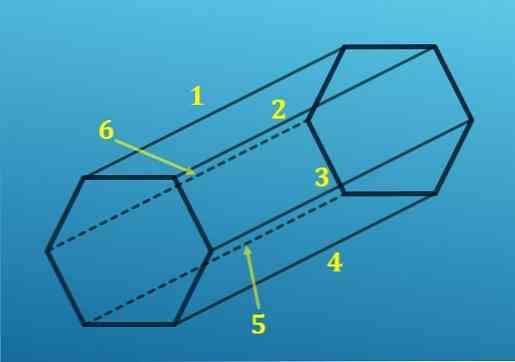
Додавањем свих ивица добијате укупно 18 ивица.
Закључак
Може се показати да је број ивица призме једнак троструком броју ивица које има полигон који има.
Према томе, петерокутна призма ће имати 3 * 5 = 15 ивица, хептагонална призма ће имати 3 * 7 = 21 ивица и на тај начин се може применити на било коју призму.
Референце
- Биллстеин, Р., Либескинд, С., & Лотт, Ј.В. (2013). Математика: приступ рјешавања проблема за наставнике основног образовања. Лопез Матеос Едиторес.
- Фрегосо, Р.С., & Царрера, С.А. (2005). Математика 3. Едиториал Прогресо.
- Галлардо, Г., & Пилар, П. М. (2005). Математика 6. Едиториал Прогресо.
- Гутиеррез, Ц.Т., & Циснерос, М. П. (2005). Трећи курс математике. Едиториал Прогресо.
- Кинсеи, Л., & Мооре, Т.Е. (2006). Симетрија, облик и простор: Увод у математику кроз геометрију (илустровано, репринт ед.). Спрингер Сциенце & Бусинесс Медиа.
- Митцхелл, Ц. (1999). Даззлинг Матх Лине Десигнс (Иллустратед ед.). Сцхоластиц Инц.
- Р., М. П. (2005). Ја цртам 6º. Едиториал Прогресо.


