Архимедов биографија, доприноси и изуми
Архимед из Сиракузе (287 а.Ц - 212 а.Ц) био је математичар, физичар, изумитељ, инжењер и грчки астроном из древног града Сиракузе, на острву Сицилија. Његов најзначајнији допринос је Архимедов принцип, развој методе ексхумације, механичка метода или стварање првог планетаријума.
Тренутно се сматра као једна од три важније фигуре из математике антике поред Еуклида и Аполонија, јер су њени доприноси значили значајне научне напретке за време у областима калкулације, физике, геометрије и астрономије. С друге стране, то га чини једним од најистакнутијих научника у историји човечанства.

Иако је познато мало детаља о његовом личном животу - а они који су познати имају сумњиву поузданост - његови доприноси су познати захваљујући низу писаних писама о његовим дјелима и постигнућима која су сачувана до данас, припадајући на кореспонденцију коју је годинама држао са пријатељима и другим математичарима тог времена.
Архимед је био познат у своје време захваљујући својим проналасцима, који су привукли пажњу његових савременика, делимично и зато што су коришћени као ратни уређаји за успешно избегавање бројних римских инвазија..
Међутим, речено је да је тврдио да је једина заиста важна ствар математика и да су његови изуми само производ забаве примењене геометрије. У потомству, његови радови у чистој математици били су много више цењени од његових изума.
Индек
- 1 Биограпхи
- 1.1 Обука
- 1.2 Научни рад
- 1.3 Сукоб у Сиракузи
- 1.4 Смрт
- 2 Научни доприноси Архимеда
- 2.1 Принцип Архимеда
- 2.2 Механичка метода
- 2.3 Објашњење закона полуге
- 2.4 Развој методе ексхумације или осиромашења за научну демонстрацију
- 2.5 Мера круга
- 2.6 Геометрија сфера и цилиндара
- 3 Изуми
- 3.1 Одометар
- 3.2 Први планетаријум
- 3.3 Архимедов вијак
- 3.4. Архимедова канџа
- 4 Референце
Биограпхи
Архимед из Сиракузе рођен је отприлике 287. године пне. О његовим раним годинама није познато много информација, мада се може рећи да је рођен у Сиракузи, граду који се сматра главном луком острва Сицилија, данас у Италији..
У то време, Сиракуза је била један од градова који су чинили такозвану Магну Грециу, која је била насељена насељеницима грчког порекла на јужном делу полуострва Италије и на Сицилији..
Нема познатих чињеница о мајци Архимеду. У односу на оца, познато је да се то звало Пхидиас и да је био посвећен астрономији. Ова информација о његовом оцу је позната захваљујући фрагменту књиге Бројач песка, написао је Архимед, у којем он спомиње име свог оца.
Хераклидес, који је био грчки филозоф и астроном, веома је волео Архимедеса и чак је написао биографију о њему. Међутим, тај документ није сачуван, тако да су све информације у њему непознате.
С друге стране, историчар, филозоф и биограф Плутарко је у својој књизи под називом Паралелни живот навео да је Архимед имао крвну везу са Хијером ИИ, тиранином који је био задужен у Сиракузи од 265. пне..
Траининг
Као резултат малог броја информација које имамо о Архимеду, не знамо са сигурношћу где је добио прву обуку.
Међутим, различити историографи су утврдили да постоји велика могућност да је Архимед био студен у Александрији, која је била најзначајнији грчки културни и наставни центар у региону..
Ова претпоставка је подржана информацијама које је понудио грчки историчар Диодоро Сицуло, који је указао да је Архимед вероватно студирао у Александрији.
Поред тога, у многим својим радовима Архимед сам спомиње и друге научнике времена чији је рад био концентрисан у Александрији, тако да се може претпоставити да се он заиста развио у том граду..
Неке од личности са којима је Архимед веровао да су у интеракцији у Александрији су географ, математичар и астроном Ератостен од Цирене, и математичар и астроном Цонон де Санос.
Породична мотивација
С друге стране, чињеница да је Архимедов отац био астроном могао је имати значајан утицај на склоности које је касније показао, јер је касније иу младости постојала посебна атракција у области науке.
Након његовог боравка у Александрији, процјењује се да се Архимед вратио у Сиракузу.
Научни рад
По повратку у Сиракузу, Архимед је почео да осмишљава различите артефакте који су му убрзо дали извесну популарност међу становницима овог града. У том периоду потпуно се посветио научном раду, произвео различите изуме и закључио неколико математичких појмова који су веома напредовали до његовог времена.
На примјер, када се посветио проучавању карактеристика чврстих закривљених и равних фигура, дошао је до појмова везаних за интегрални и диференцијални рачун, који је касније развијен..
Такође, Архимед је био онај који је дефинисао да запремина повезана са сфером одговара дупло већој величини цилиндра који га садржи, и да је онај који је изумео композитну ременицу, на основу својих открића о закону полуге..
Сукоб у Сиракузи
Током 213. пне, римски војници су ушли у град Сиракузу и опколили њене досељенике како би их предали.
Ову акцију водили су војни и грчки политичар Марко Цлаудио Марцело у оквиру Другог пунског рата. Касније је био познат као Римски мач, пошто је завршио освајањем Сиракузе.
Усред сукоба, који је трајао двије године, становници Сиракузе су се храбро и жестоко борили против Римљана, а Архимед је одиграо веома важну улогу, с обзиром на то да се посветио стварању алата и инструмената који су помогли поразити Римљане.
Коначно, Марцо Цлаудио Марцело је преузео град Сиракузу. Пре велике интелектуалности Архимеда, Марцело је наредио да не буду повређени или убијени. Међутим, Архимед је убијен у рукама римског војника.
Смрт
Архимед је умро у 212. години пне. Више од 130 година након његове смрти, 137. године пре нове ере, писац, политичар и филозоф Марцо Тулио Цицеро заузимао је положај у управи Рима и желио је да пронађе Архимедову гробницу..
Овај задатак није био лак, јер Цицеро није могао наћи никога да наведе тачно мјесто. Међутим, коначно га је добио, врло близу врата Агригента и у жалосним условима.
Цицерон је очистио гробницу и открио да је он уписан са сфером унутар цилиндра, као референцу на откриће о волумену који је Архимед направио прије неког времена..
Верзије о његовој смрти
Прва верзија
Једна од верзија каже да је Архимед био усред решавања математичког проблема када му је пришао римски војник. Речено је да га је Архимед могао неко вријеме замолити да ријеши проблем, тако да би га војник убио.
Друга верзија
Друга верзија је слична првој. Прича се да је Архимед решавао проблем математике када је дошло до заузимања града.
Један римски војник је ушао у његов комплекс и наредио му да се састане са Марчелоом, а Архимед је одговорио да мора ријешити проблем на којем је прво радио. Војник се узрујао због тог одговора и убио га.
Трећа верзија
Ова хипотеза указује да је Архимед имао у својим рукама велику разноликост инструмената типичних за математику. Тада га је видио војник и помислио је да може носити вриједне предмете, па га је убио.
Четврта верзија
Ова верзија показује да је Архимед био чучао близу земље, размишљајући о плановима које је проучавао. Очигледно, римски војник је дошао са стражње стране и, несвјестан да је то Архимед, пуцао је у њега.
Научни доприноси Архимеда
Принцип Архимеда
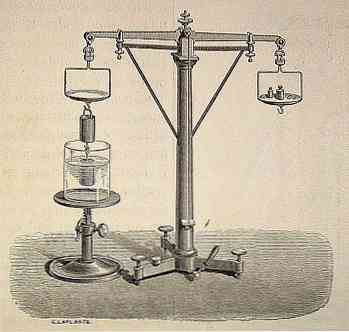
Принцип Архимеда модерна наука сматра једним од најважнијих наслеђа из античког доба.
Кроз историју, и усмено, објављено је да је Архимед дошао до свог открића случајно захваљујући краљу Хиерону који је наручио да види да ли је златна круна, коју је послао да производи од њега, направљен само од злата. чист и није садржавао ниједан други метал. Морао сам ово да изведем без уништења круне.
Речено је да је, док је Архимед медитирао како ријешити овај проблем, одлучио да се окупа, а кад је ушао у каду, схватио је да се вода повећала кад се у њу уронио..
На тај начин, он би открио научни принцип да "свако тело које је потпуно или делимично уроњено у течност (течност или гас) прима навише навише, једнако тежини течности која је избачена из објекта".
Овај принцип значи да течности испољавају узлазну силу - гурање према горе - на било који предмет уроњен у њих, и да је количина ове силе гурања једнака тежини течности која је потиснута потопљеним телом, без обзира на његову тежину..
Објашњење овог принципа описује феномен флотације и налази се у његовом Уговор о пловним објектима.
Принцип Архимеда је у великој мери примењен у потомству за плутање објеката масовне употребе као што су подморнице, бродови, спасиоци и балони.
Мецханицал метход
Још један од најважнијих доприноса Архимеда науци био је укључивање чисто механичког-то јест, техничког-метода у расуђивање и аргументовање геометријских проблема, што је значило невиђен начин решавања овог типа проблема за време.
У контексту Архимеда, геометрија је сматрана искључиво теоријском науком, а уобичајено је да се чиста математика спустила ка другим практичним наукама у којима се могу примијенити њени принципи..
Због тога се данас сматра претечом механике као научне дисциплине.
У писању у којем математичар излаже нови метод свом пријатељу Ератостену, указује се да то дозвољава да се проблеми математике обрађују преко механике, и да је нешто лакше изградити демонстрацију геометријске теореме ако је већ имати неко претходно практично знање, ако немате никакву идеју о томе.
Ова нова метода истраживања коју је спровео Архимед постао би претеча неформалне фазе откривања и формулисања хипотеза модерне научне методе..
Објашњење закона полуге
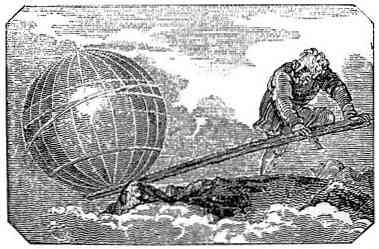
Док је полуга једноставна машина која се користила много раније од Архимеда, он је формулисао принцип који објашњава његово функционисање у његовој расправи о равнотежи авиона.
У формулацији овог закона, Архимед успоставља принципе који описују различито понашање полуге при постављању два тела на њу, у зависности од њене тежине и удаљености од тачке ослонца..
На овај начин он истиче да су два тела која се могу мерити (пропорционална), смјештена на полуги, балансирана када су на размацима обрнуто пропорционална њиховој тежини..
На исти начин, немерљива тела (која се не могу мерити) то чине, али овај закон је био видљив само Архимеду са телима првог типа..
Његова формулација принципа полуге је добар примјер примјене механичке методе, будући да према њој објашњава у писму упућеном Доситеу, да је овај откривен у првом тренутку методама механике који се примјењују у пракси.
Касније их је формулисао методама геометрије (теоријским). Из овог експеримента на телима такође је откривен појам центра гравитације.
Развој методе ексхумације или исцрпљивања за научну демонстрацију
Исцрпљеност је метода која се користи у геометрији и састоји се од апроксимације геометријских фигура чија је површина позната, помоћу натписа и описа, на другом чија је површина предвиђена за познавање..
Иако Архимед није био творац ове методе, он га је мајсторски развио, успјевши да помоћу њега израчуна прецизну вриједност Пи.
Архимед, користећи методу ексхумације, уписане и описане шестерокуте до обима пречника 1, редукујући до апсурда разлику између површине шестерокута и обима.
Да би то урадио, он је раздвојио шестерокуте стварајући полигоне до 16 страна, као што је приказано на претходној слици.
На тај начин је дошао до тога да одреди да је вредност пи (односа између дужине круга и њеног пречника) између вредности 3.14084507 ... и 3.14285714 ... .
Архимед је мајсторски користио метод екхауцион зато што је не само успио да апроксимира израчунавање вредности Пи са маргином грешке прилично ниском, и стога пожељним, већ и зато што је Пи ирационалан број, кроз овом методом и добијеним резултатима постављени су темељи који би проклијали у инфинитезималном рачунском систему, а касније у савременом интегралном рачуну.
Мера круга
Да би одредио подручје круга, Архимед је користио метод који се састојао од цртања квадрата који се уклапа тачно унутар круга.
Знајући да је подручје квадрата сума његових страна и да је подручје круга било веће, почео је радити на добивању апроксимација. То је учинио замјеном квадрата са 6-страним полигоном, а затим радом са сложенијим полигонима.
Архимед је био први математичар у историји који је приступио озбиљном прорачуну броја Пи.
Геометрија сфера и цилиндара
Међу девет разматрања која се баве Архимедовим радом из математике и физике, постоје два свеска о геометрији сфера и цилиндара..
Овај рад се бави утврђивањем да је површина било које сфере полупречника четири пута већа од њене највеће кружнице, а да је обим кугле две трећине круга цилиндра у коме је уписан.
Инвентионс
Одометар
Такође познат као километри, то је био изум овог чувеног човека.
Овај уређај је изграђен на принципу точка који, када се окрене, активира зупчанике који омогућавају израчунавање пређене удаљености..
Према том истом принципу, Архимед је дизајнирао неколико типова одометара за војне и цивилне сврхе.
Први планетаријум
На основу сведочења многих класичних писаца као што су Цицерон, Овид, Цлаудиан, Марциано Цапела, Цасиодоро, Секто Емпирицо и Лацтантиус, многи научници сада приписују Архимеду стварање првог елементарног планетаријума.
То је механизам који се састоји од низа "сфера" које су имитирале кретање планета. До сада детаљи овог механизма нису познати.
Према Цицерону, планетаријуми које је саградио Архимед су били два. У једној од њих представљена је земља и разне констелације у близини.
У другој, са једном ротацијом, Сунце, Месец и планете су правили своје независне покрете у односу на фиксне звезде на исти начин као у стварном дану. У потоњем, поред тога, могу се посматрати и узастопне фазе и помрачења Месеца.
Вијак Архимеда
Архимедов вијак је уређај који се користи за транспорт воде од дна до врха кроз нагиб, користећи цијев или цилиндар.
Према грчком историчару Диодору, захваљујући овом проналаску омогућено је наводњавање плодних земљишта које се налазе дуж реке Нил у древном Египту, јер су традиционални алати захтевали огроман физички напор који је исцрпио раднике..
Кориштени цилиндар има унутар вијака исте дужине, који одржава међусобно повезан систем пропелера или ребара који обављају ротациони покрет који се ручно покреће помоћу ротирајуће полуге..
На тај начин, хеликси успијевају гурнути било коју супстанцу одоздо према горе, формирајући неку врсту бесконачног круга.
Канџа Архимеда
Архимедова канџа, или гвоздена рука, као што је познато, била је једно од најстрашнијих ратних оружја које је створио овај математичар, постајући најважнији за обрану римских инвазија на Сицилији..
Према истраживању које су провели професори Универзитета Дрекел Цхрис Роррес (Одјел за математику) и Харри Харрис (Одјел за грађевинарство и архитектуру), то је била велика полуга која је имала куку за причвршћивање на полугу ланцем који је висио са њега.
Кроз полугу је манипулисана кука тако да је пала на непријатељски брод, а циљ је био да се закачи и подигне до те мјере да би се, када би је ослободила, могла потпуно преврнути или погодити стијене на обали..
Роррес и Харрис представили су на симпозијуму "Машине и изванредне структуре антике" (2001), минијатурни приказ овог артефакта под називом "Страшна ратна машина: Изградња и рад Архимедове" Гвоздене руке "
За реализацију овог рада ослањали су се на аргументе древних историчара Полибија, Плутарка и Тита Ливија..
Референце
- АССИС, А. (2008). Архимед, центар гравитације и први закон механике. Приступљено 10. јуна 2017. на боурабаи.ру.
- ДИЈКСТЕРХУИС, Е. (1956). Арцхимедес [на мрежи]. Приступљено 9. јуна 2015. године на Ворлд Виде Вебу: боокс.гоогле.цо.ве/боокс.
- МОЛИНА, А. (2008). Метода истраживања Архимеда из Сиракузе: интуиција, механика и ексхумација [на мрежи]. Приступљено 10. јуна 2017. на Ворлд Виде Вебпродуцционциентифица.луз.еду.
- О'ЦОННОР, Ј. & РОБЕРТСОН, Р. (1999). Арцхимедес оф Сирацусе [онлине]. Приступљено 9. јуна 2017. у хистори.мцс.ст-анд.ац.ук.
- ПАРРА, Е. (2009). Архимед: његов живот, дела и доприноси модерној математици [онлине]. Преузето 9. јуна 2017. на лфунес.униандес.еду.цо.
- КУИНН, Л. (2005). Арцхимедес оф Сирацусе [онлине]. Приступљено 9. јуна 2017. године на адреси матх.уцденвер.еду.
- РОРРЕС, Ц. & ХАРРИС, Х. (2001). Страшна ратна машина: Изградња и рад Архимедове 'Гвоздене руке' [онлине]. Приступљено 10. јуна 2017. године на адреси цс.дрекел.еду.
- ВИТЕ, Л. (2014). Принцип Архимеда [на мрежи]. Ретриевед он Јуне 10, 2017 ат репоситори.уаех.еду.мк.


