Формуле за угаоно померање и решене вежбе

Тхе кутно померање он се генерише када се објекат креће пратећи пут или путању која има облик круга. Она се разликује од расељавања; док угаоно померање мери преваљени угао, померање мери удаљеност.

Да би се израчунао угаони померај објекта који се креће дуж обима могу се користити два начина: ако је почетни и коначни угао познат, тада ће угаоно померање бити одузимање између крајњег угла и почетног угла..

Ако је позната дужина помака (дужина кружног лука) и полупречник обима, тада је кутни помак дат као θ = л / р..

Индек

• 1 Формуле
• 2 Вежбе
  • 2.1 Прва вежба
  • 2.2 Друга вежба
  • 2.3 Трећа вежба
• 3 Референце

Формуле

Да бисте добили горе описане формуле можете видети следеће слике:

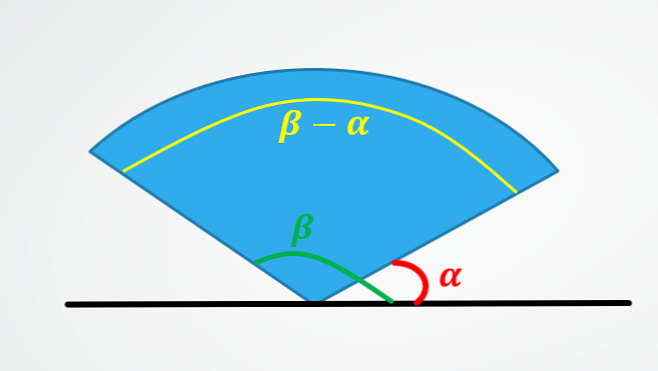
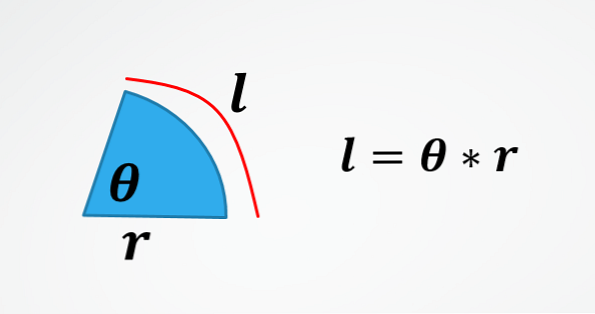
Први показује зашто је кутно померање једнако одузимању коначног угла минус почетни угао.

У другој слици је формула за дужину лука кружнице. Дакле, брисањем θ добијате формулу описану на почетку.

Вежбе

У наставку су наведене неке вежбе где треба применити дефиницију угловног померања и где се користе горе описане формуле.

Прва вежба

Јуан је трчао на удаљености од 35 метара на кружној стази чији је радијус једнак 7 метара. Израчунајте кутни помак који је направио Јуан.

Решење

Пошто је удаљеност путеног лука и полупречника обода позната, друга формула се може применити да би се знало угаоно померање које је направио Јуан. Користећи горе описану формулу имате θ = 35/7 = 5 радијана.

Друга вежба

Ако имате да је Марио путовао у свом возилу пола кружне тркаће стазе, који је кутни помак који је Марио учинио??

Решење

У овој вјежби ће се примијенити прва формула. Пошто је познато да је Марио превалио половину стазе, може се претпоставити да је стартао у углу 0 ° и када је стигао до средине круга, прешао је 180 °. Дакле, одговор је 180 ° -0 ° = 180 ° = π радијана.

Трећа вежба

Марија има кружни базен. Ваш пас трчи око базена на удаљености од 18 метара. Ако је радијус базена 3 метра, колики је кутни помак од Маријине маскоте??

Решење

Пошто је базен кружан и знате његов радијус, можете наставити са употребом друге формуле.

Познато је да је радијус једнак 3 метра, а удаљеност коју је превалио љубимац износи 18 метара. Због тога је извршено угаоно померање једнако θ = 18/3 = 6 радијана.

Референце

1. Басто, Ј.Р. (2014). Математика 3: Основна аналитичка геометрија. Патриа Едиториал Гроуп.
2. Биллстеин, Р., Либескинд, С., & Лотт, Ј.В. (2013). Математика: приступ рјешавања проблема за наставнике основног образовања. Лопез Матеос Едиторес.
3. Булт, Б., & Хоббс, Д. (2001). Матх лекицон (илустровано ед.). (Ф. П. Цадена, Трад.) Едитионс АКАЛ.
4. Цаллејо, И., Агуилера, М., Мартинез, Л., & Алдеа, Ц. (1986). Математика Геометри Реформа горњег циклуса Е.Г.. Министарство образовања.
5. Сцхнеидер, В., & Сапперт, Д. (1990). Практични технички приручник за цртање: увод у основе индустријског техничког цртања. Реверте.
6. Тхомас, Г. Б., & Веир, М. Д. (2006). Израчунавање: неколико варијабли. Пеарсон Едуцатион.