Колико осовина симетрије има круг?

Тхе оси симетрије круга Они су бесконачни. Ове осовине су оне које дијеле било који геометријски облик на два точно једнака пола.

А круг се састоји од свих тачака чија је удаљеност до фиксне тачке мања или једнака одређеној вредности "р".

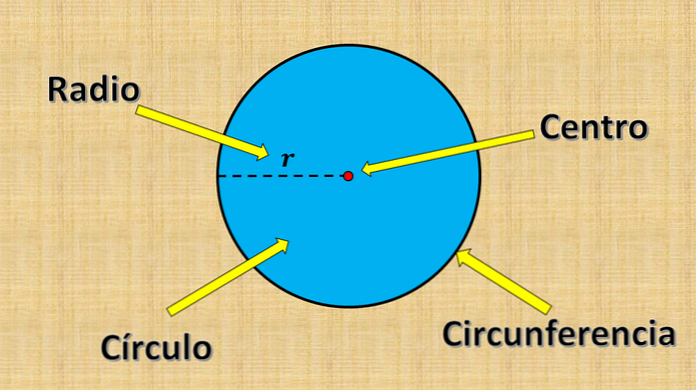
Горе наведена фиксна тачка се зове центар, а вредност "р" се зове радијус. Радијус је највећа удаљеност између тачке на кругу и центра.

Са друге стране, било који сегмент чије су крајеви на ивици круга (обим) и пролазећи кроз центар се назива пречник. Његово мерење је увек једнако двоструком радијусу.

Круг и обим

Немојте бркати круг са кругом. Обим се односи само на тачке које су на удаљености "р" од центра; то јест, само ивица круга.

Међутим, када тражите осе симетрије, то је индиферентно ако радите са кругом или кругом.

Шта је ос симетрије?

Оса симетрије је линија која дели два једнака дела одређеном геометријском фигуром. Другим речима, ос симетрије делује као огледало.

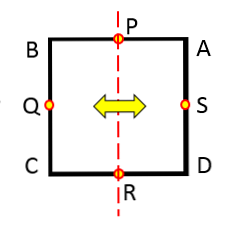
Осовине симетрије круга

Ако посматрате било који круг, без обзира на његов радијус, можете видети да није свака линија која прелази то оса симетрије.

На пример, ниједна линија која је нацртана на следећој слици није ос симетрије.

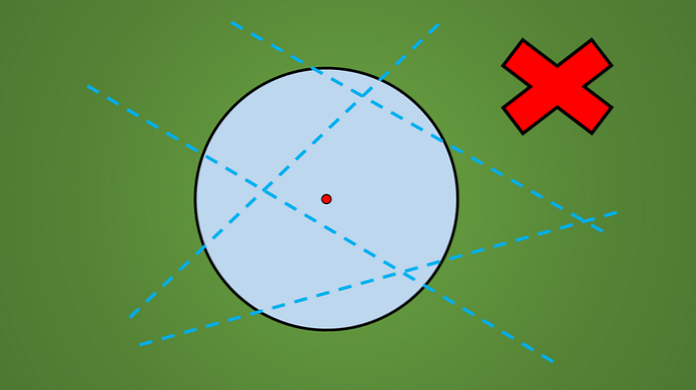
Лак начин да се провери да ли је линија оса симетрије или не, треба да одражава окомиту геометријску цифру на супротну страну линије.

Ако се рефлексија не уклапа са оригиналном фигуром, онда та линија није ос симетрије. Следећа слика илуструје ову технику.

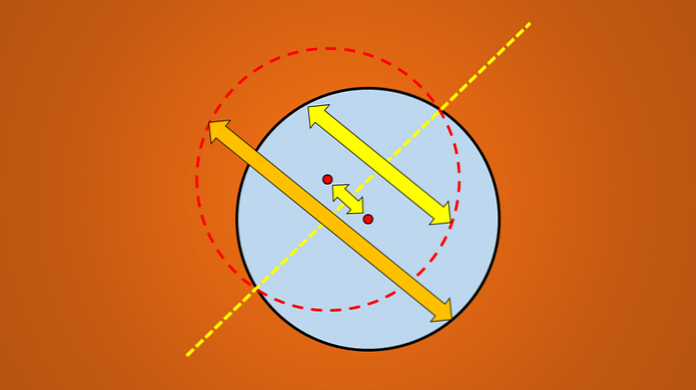
Али, ако се разматра следећа слика, добро је познато да је нацртана линија оса симетрије круга.

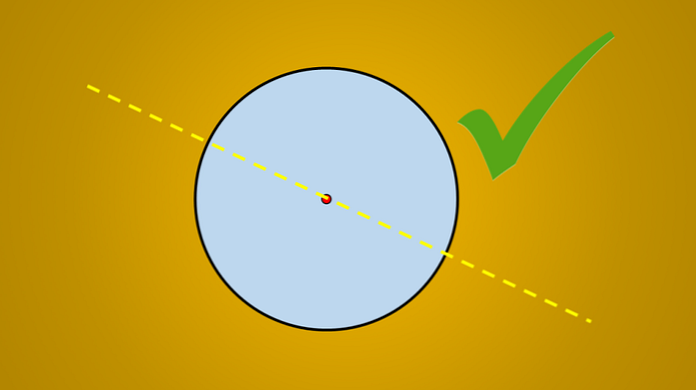
Питање је: има ли више осе симетрије? Одговор је да. Ако окренете ову линију 45 ° у смеру супротном од казаљке на сату, добијена линија је такође и ос симетрије круга.

Исто се дешава ако ротирате за 90 °, 30 °, 8 ° и, уопште, било који број степени.

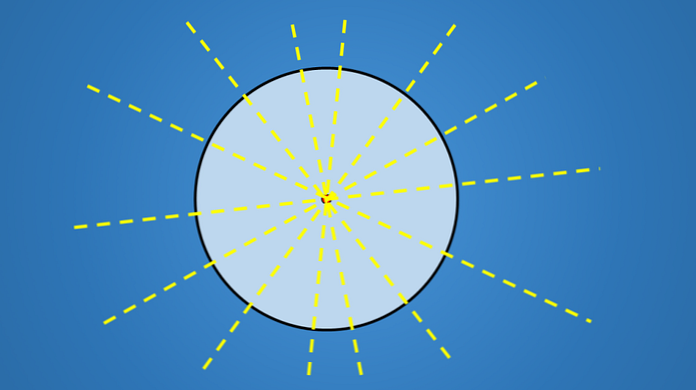
Важна ствар код ових линија није нагиб који имају, већ сви пролазе кроз средиште круга. Дакле, свака линија која садржи пречник круга је ос симетрије.

Дакле, пошто круг има бесконачан број пречника, онда има бесконачан број оса симетрије.

Друге геометријске фигуре, као што су троугао, четвороугао, петерокут, шестерокут или било који други полигон, имају коначан број оса симетрије.

Разлог зашто круг има бесконачан број симетријских осе је да нема стране.

Референце

1. Басто, Ј.Р. (2014). Математика 3: Основна аналитичка геометрија. Патриа Едиториал Гроуп.
2. Биллстеин, Р., Либескинд, С., & Лотт, Ј.В. (2013). Математика: приступ рјешавања проблема за наставнике основног образовања. Лопез Матеос Едиторес.
3. Булт, Б., & Хоббс, Д. (2001). Матх лекицон (илустровано ед.). (Ф. П. Цадена, Трад.) Едитионс АКАЛ.
4. Цаллејо, И., Агуилера, М., Мартинез, Л., & Алдеа, Ц. (1986). Математика Геометри Реформа горњег циклуса Е.Г.. Министарство образовања.
5. Сцхнеидер, В., & Сапперт, Д. (1990). Практични технички приручник за цртање: увод у основе индустријског техничког цртања. Реверте.
6. Тхомас, Г. Б., & Веир, М. Д. (2006). Израчунавање: неколико варијабли. Пеарсон Едуцатион.